1、数学上的“七桥问题”怎么解答

这其实是一个一笔画的问题。

解法如下：

1.凡是由偶点组成的连通图，一定可以一笔画成。画时可以把任一偶点为起点，最后一定能以这个点为终点画完此图。

⒉凡是只有两个奇点的连通图（其余都为偶点），一定可以一笔画成。画时必须把一个奇点为起点，另一个奇点终点。

⒊其他情况的图都不能一笔画出。(奇点数除以二便可算出此图需几笔画成。)

七桥所成之图形中，没有一点含有偶数条数，因此上述的任务无法完成.

2、七桥问题 的答案是什么？？？

答案是无解的，你要记住，七桥问题即：能否笔不离纸，不重复地一笔画完整个图形。“一笔画”问题，数学分析：一笔画有起点和终点，起点和终点重合的图形称为封闭图形，否则便称为开放图形。除起点和终点外，一笔画中间可能出现一些曲线的交点。只有当笔沿着一条弧线到达交点后，又能沿着另一条弧线离开，也就是交汇于这些点的弧线成双成对时，一笔画才能完成，这样的交点就称为“偶点”。如果交汇于这些点的弧线不是成双成对，也就是有奇数条，则一笔画就不能实现，这样的点又叫做“奇点” 结论：若是一个一笔画图形，要么只有两个奇点，也就是仅有起点和终点，这样一笔画成的图形是开放的；要么没有奇点，也就是终点和起点连接起来，这样一笔画成的图形是封闭的。由于七桥问题有四个奇点，所以要找到一条经过七座桥，但每座桥只走一次的路线是不可能的。

3、七桥问题一笔画答案

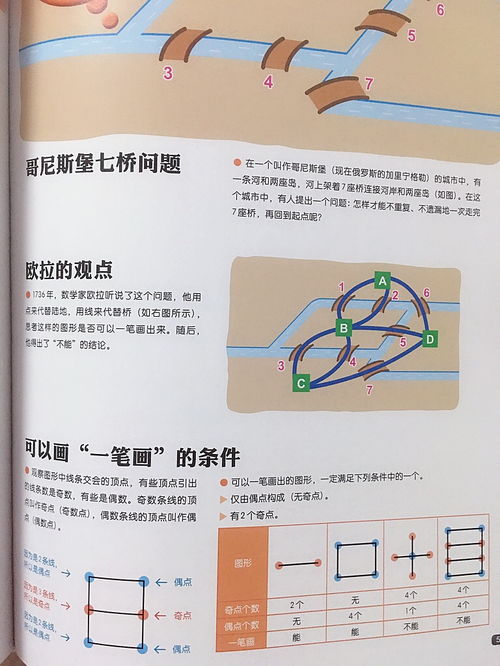
1736年，欧拉证实：七桥问题的走法根本不存在。同时，他发表了“一笔画定理”：一个图形要能一笔画完成必须符合两个条件，即图形是封闭联通的和图形中的奇点（与奇数条边相连的点）个数为0或2。当奇点个数为0时，即图形中只有偶点（与偶数条边相连的点）时，从任一点开始，一笔画完回到此点；当奇点个数为2时，从一奇点开始，一笔画完回到另一奇点。

4、七桥问题一笔画图解怎么走顺序

七桥问题一笔画图解怎么走顺序

大数学家欧拉把它转化成一个几个问题一笔画问题。

上图中的七条线代表七座桥,红点代表它们相交的点。欧拉发现只有当笔沿着一条弧线到达交点后，又能沿着另一条弧线离开，也就是交汇于这些点的弧线成双成对时，一笔画才能完成，这样的交点就称为“偶点”。如果交汇于这些点的弧线不是成双成对，也就是有奇数条弧线，则一笔画就不能实现，这样的点又叫做“奇点”。

欧拉通过分析，得到了下面的结论：若是一个一笔画图形，要么只有两个奇点，也就是仅有起点和终点，这样一笔画成的图形是开放的；要么没有奇点，也就是终点和起点连接起来，这样一笔画成的图形是封闭的。由于七桥问题有四个奇点，所以要找到一条经过七座桥，但每座桥只走一次的路线是不可能的。有名的“哥尼斯堡七桥问题”就这样被欧拉解决了。

请添加微信号咨询：19071507959

在线报名

上一篇：七根火柴,《七根火柴》原文是什么？

下一篇：七步上栏,刘翔七步上栏是什么意思