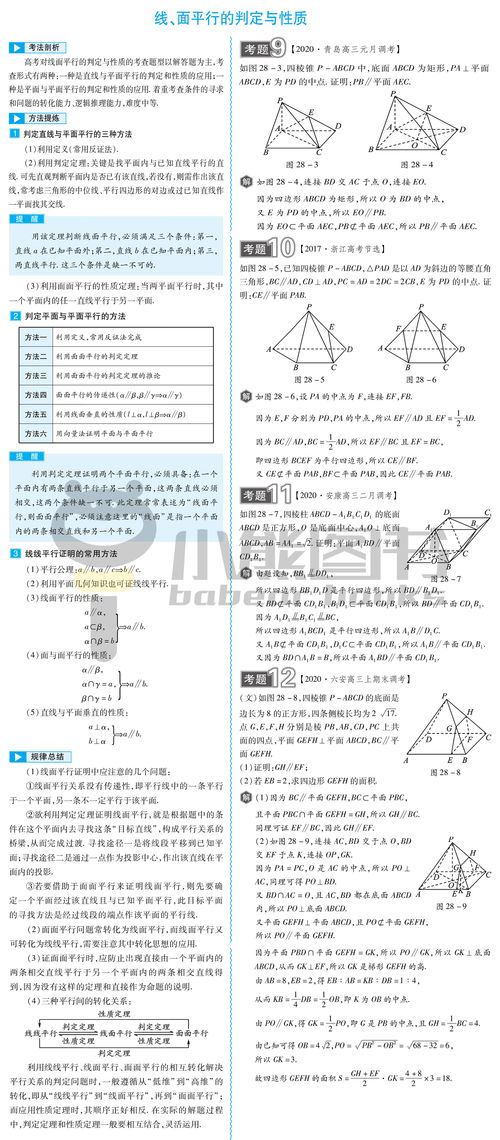
1、面面垂直的判定

面面垂直的判定定理：一个平面过另一平面的垂线，则这两个平面相互垂直。如果一个平面的垂线平行于另一个平面，那么这两个平面互相垂直。如果两个平面的垂线互相垂直，那么这两个平面互相垂直。

面面垂直的判定定理

1、在一个平面内做2条相交直线，另一个平面内有一条直线垂直于这两条相交直线，则面面垂直。

2、如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面，则面面垂直。

3、如果一个平面经过另一平面的垂线，则这两个平面相互垂直。

面面垂直的证明方法

1、定义法：如果两个平面所成的二面角为90°，那么这两个平面垂直。

2、判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。

3、如果一个平面内任意点在另外一个平面的射影均在这两个平面的交线上，那么垂直。

4、如果N个互相平行的平面有一个垂直于一个平面，那么其余平面均垂直这个平面。

2、面面垂直的判定定理是什么？

共三个定理：

1、在一个平面内做2条相交直线，另一个zhi平面内有一条直线垂直于这两条相交直线，则面面垂直。

2、如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。 面面垂直。

3、如果一个平面经过另一平面的垂线,则这两个平面相互垂直。

一个平面过另一平面的垂线，则这两个平面相互垂直。

几何描述：若a⊥β，a⊂α，则α⊥β

证明：任意两个平面关系为相交或平行，设a⊥β，垂足为P，那么P∈β

∵a⊂α，P∈a

∴P∈α

即α和β有公共点P，因此α与β相交。

设α∩β=b，∵P是α和β的公共点

∴P∈b

过P在β内作c⊥b

∵b⊂β，a⊥β

∴a⊥b，垂足为P

又c⊥b，垂足为P

∴∠aPc是二面角α-b-β的平面角

∵c⊂β

∴a⊥c，即∠aPc=90°

根据面面垂直的定义，α⊥β

3、面面垂直的判定定理是什么

4、面面垂直的条件是什么

1.如果两个平面相互垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。

2.如果两个平面相互垂直，那么经过第一个平面内的一点作垂直于第二个平面的直线在第一个平面内。

3.如果两个相交平面都垂直于第三个平面，那么它们的交线垂直于第三个平面。

4.如果两个平面互相垂直，那么一个平面的垂线与另一个平面平行。

直线与平面垂直的判定定理（线面垂直定理）：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。

推论1：如果在两条平行直线中，有一条直线垂直于一个平面，那么另一条直线也垂直于这个平面。

推论2：如果两条直线垂直于同一个平面，那么这两条直线平行。

"/>

请添加微信号咨询：19071507959

在线报名

上一篇：面面垂直,面面垂直

下一篇：暂无